
Here are results of the larger Hermann Grid, reproduced here for convenience.

Figure 7
Reviewing the results below, the grid is twice as big in each dimension and each successive receptive field has the same relationship. So Figure 9 shows the same pattern and Figure 4 and Figure 10 shows the same pattern as Figure 5. The new pattern is shown in Figure 8. Here actually is a classic graph that shows the perception of Hermann Grid.
se = 2; si = 6
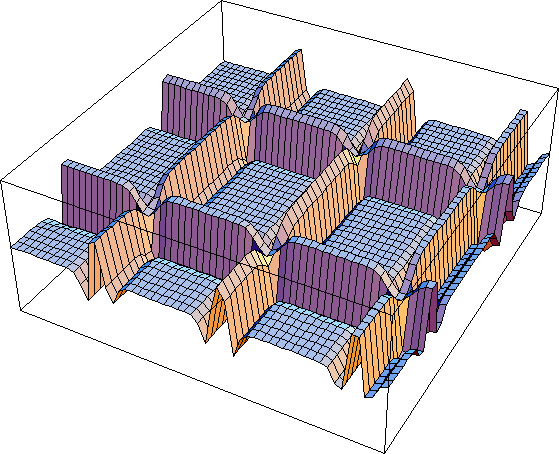
Figure 8

Figure 8a shows the three situations for the position of a receptive field we have considered before. It shows that truly in this situation, the inhibition is greatest when the receptive field is in the center of the intersection and thus it give the lowest response. So is it possible that the Hermann Grid illusion is driven by receptive fields that have centers smaller than the lines and that is how the response of receptive fields that have centers larger than the lines? I don't think so based on one basic observation (I would love email confirming or disconfirming my experience here). Looking back at the two squares, the effect is weakest in the fovea where the receptive fields are the smallest. For me, the effect does not exist an normal viewing distances (<2' for my monitor) for the larger grid in the fovea. Since the receptive fields are the smallest in the fovea, then the effect should be the strongest there, and the reverse is the case. So there must be some other mechanism besides mere output level of these cells that drives this outcome.
se = 4; si = 12
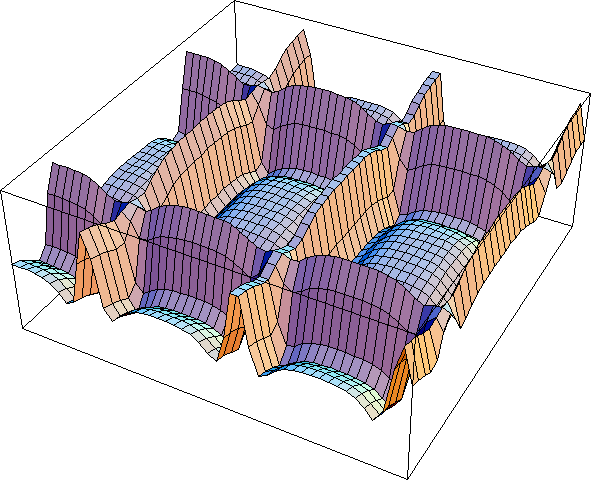
Figure 9
se = 8; si = 24
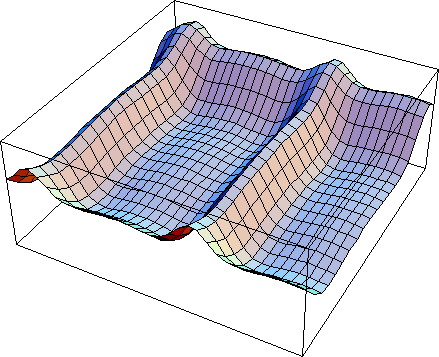
Figure 10