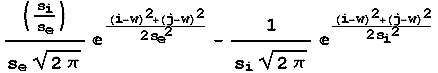
Here is the equation for the 2-D receptive field:
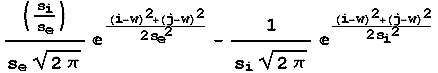
w = the radius of the receptive field
se = the standard deviation of
the excitatory center
si = the standard
deviation of the inhibitory surround
i,j = the position within
the receptive field of the receptor
In this instantiation of the model, the
width is set to 3*si, or three times the standard deviation of the
surround which is inhibitory in this cell. The one odd value from the
standard DOG equation is the ![]() ratio
or weight at the beginning of the excitatory receptive field. This was
necessary to balance out the increased surround area going from the 1
dimensional to the 2 dimensional version of the model. By adding the
second dimension, the surround grows at a greater rate since it is
larger (area of a circle is Pr2). A
linear adjustment is all that is necessary because they were balanced in one
dimension and only need to compensate for the second dimension. The
resulting map of sensitivity is shown below.
ratio
or weight at the beginning of the excitatory receptive field. This was
necessary to balance out the increased surround area going from the 1
dimensional to the 2 dimensional version of the model. By adding the
second dimension, the surround grows at a greater rate since it is
larger (area of a circle is Pr2). A
linear adjustment is all that is necessary because they were balanced in one
dimension and only need to compensate for the second dimension. The
resulting map of sensitivity is shown below.
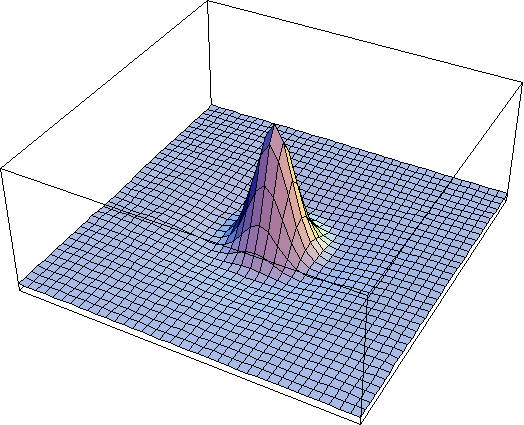
The inhibitory region is not as visible due the the greater amplitude of the central region.
This page illustrates how the model works in a very basic way.
If you have Mathematica you can download the notebook with this basic model and use it here.