

Figure 1 Figure 2
Look at the figures below. They are classic examples of the Hermann Grid. The intersections appear darker than the regions between just two squares. These two grids only differ in that the grid is on a spatial scale of twice the size on the right.


Figure
1
Figure 2
The standard explanation for this outcome is shown below (see Coren, Ward and Enns, 1999, p. 290 for an example).

Figure 3
The explanation runs that when the receptive field is at an intersection, the surround has more inhibition than when it falls on the line between two squares. Expecting to see this outcome, I ran both of these figures through the model with three separate sizes of of receptive fields:
| se | si |
| 2 | 6 |
| 4 | 12 |
| 8 | 24 |
Each receptive field covers a region of the retina that is twice the previous one, shifting its range of spatial frequencies that it is sensitive to, down by an octave. The reason for the three receptive fields is to mimic the fact that there are different sizes of receptive fields in the eye. The ranges are picked at random at this time and not for physiological verisimilitude.
Here are the successive output for Figure 1. This and the following retinal output figures are contour plots where the x and y dimensions indicate different ganglion cells and the height of the graph (the z dimension) shows the level of activity of that cell. The higher the value the more active that cell according to the model.
se = 2; si = 6
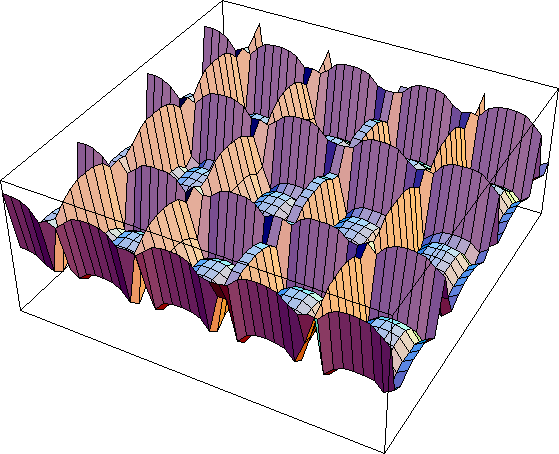
Figure 4
By and large this figure seems to show what is expected. The intersections are actually lower than the middle of the rows, but the lowest point is not right in the intersection but at the edges of the intersection (Figure 4a).

Figure 4a
As can be seen, that is expected is you look at the amount of inhibition when the receptive field is at the edge of an intersection vs. when it is in the middle of the intersection. the situation is perhaps more surprising for the larger receptive field shown below in Figure 5. In this case the peak response is at the intersection. Figure 5a illustrates why this might be. At the intersections, the central region actually gets more excitation in the central region since it this region is much larger than the width of the line. This is not what is expected and suggests that our perception moves in the opposite direction of the output of cells that are larger than the width of the lines separating the squares in the Hermann Grid. Finally, Figure 6 shows what happens with the largest receptive fields and only general features are observed, as expected. The results for the wider grid are shown here with a tentative interpretation of the findings.
se = 4; si = 12
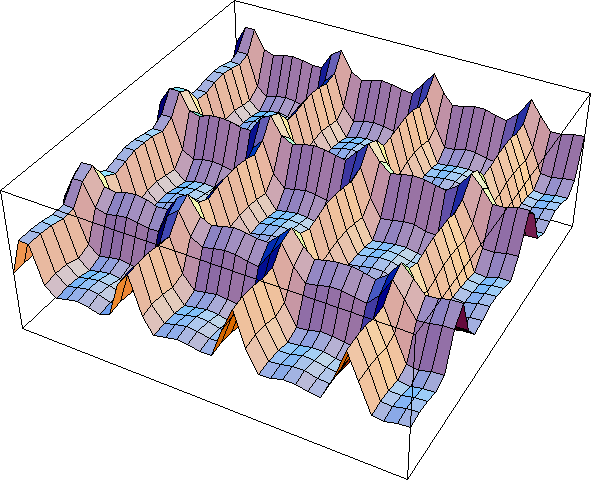
Figure 5

se = 8; si = 24
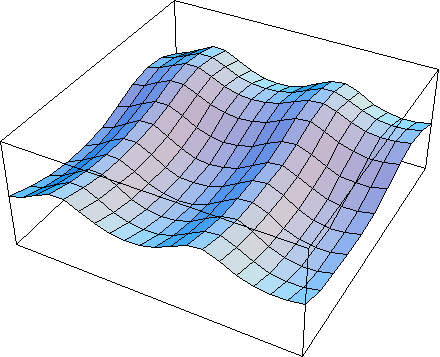
Figure 6